Supervisor
Professor Nik Cunniffe
Brief Summary
This project focuses on using mathematical models to develop strategies to extend the useful lifetime of fungicides. Part of the project will concentrate on extending a recently developed model, in fact the first model of polygenic fungicide resistance (Taylor & Cunniffe (2022a)), to include spatial effects, economics, grower behaviour and risk aversion. That model was originally developed for Septoria leaf blotch on winter wheat (caused by Zymoseptoria tritici), but the model will also be re-fitted to data on at least one other crop pathogen system, to allow the robustness of the conclusions to be properly understood.
Importance of Research
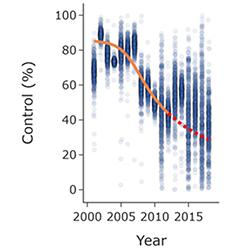
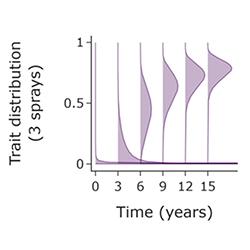
Chemical disease control exerts very strong selection pressures on plant pathogens. This promotes the evolution of resistant pathogens, which threaten crop yields and even food security. Resistance management, i.e., optimising fungicide deployment to delay the emergence or spread of resistant pathogen strains, has therefore been studied for decades. However, largely for reasons of mathematical tractability, almost all work has been done for simple models, with fungicide resistance modelled as a monogenic trait. This does not match reality, since resistance to most chemicals is polygenic, characterised by small, gradual shifts in the make-up of the pathogen population, with multiple genetic changes accumulating slowly over time. Although an initial model of this type of fungicide resistance has very recently been introduced and fitted to data, many questions are unexplored. This project focuses on finding some answers!
Project Summary
A recently completed PhD project in my laboratory developed the first model of polygenic fungicide resistance, fitted to the economically important wheat disease, Septoria leaf blotch. By extending this model to understand how polygenic fungicide resistance can be managed at landscape scales in time and space, while accounting for economics, decision support systems and grower behaviour, this project will lead to management recommendations applicable across a wide range of crop disease systems.
What will the successful application do?
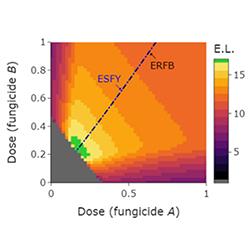
This project is based entirely on developing, fitting and using mathematical models. The project will start by focusing on a recently developed model of polygenic fungicide resistance (Taylor & Cunniffe (2022a)). The first question is how chemical sprays should optimally be combined, and whether fungicide with different modes of action should be deployed as a mixture (i.e., simultaneously) or in alternation (i.e., sequentially in separate sprays). The broad question has been debated for decades, even in the monogenic case (Taylor & Cunniffe (2022b)). An extension to the more realistic case of polygenic resistance is sorely required. The current model omits spatial aspects of pathogen spread, acknowledged to be an important factor in a range of modelling contexts (Cunniffe & Gilligan (2020)). Therefore, the next step will be to include space, considering how fungicide resistance spreads through a population of growers’ fields. Arguably more importantly, since the resistance management decisions made by any grower affect all other growers, the model also omits grower behaviour. Recent work from my laboratory shows how plant disease epidemiology and game theory can be brought together in a single model framework (Murray-Watson et al (2022)), and the models will be extended to include this. Farmers and their agronomists are also notoriously risk-averse, although they do sometimes rely on decision support systems to predict likely disease pressures and so necessary levels of chemical input (Lazaro et al. (2021). This will also be included. Finally, the robustness of our conslusions will be assessed by fitting the model to data from at least one other pathosystem, most likely late blight of potato and tomato (caused by Phytophthora infestans).
Training Provided
The student would learn i) mapping a complex biological system to a parsimonious mathematical model; ii) modern methods for simulating epidemiological models; iii) high performance computing, via use of the university’s HPC cluster; iv) experience of applying mathematics to a biological system; v) methods of fitting complex mathematical models to spatio-temporal data
The project would be well suited to a student with a background in mathematics, engineering, physics or theoretical ecology, ideally with prior knowledge of computer programming, motivated to transition to work on biological problems. However, students with a background in wet-lab biology have enjoyed and been very successful in my laboratory in the past. Any such candidates with a strong interest in making a transition to mathematical modelling are very much encouraged to get in touch to discuss.