Supervisor
Professor Nik Cunniffe
Brief Summary
This project will extend previous work in my laboratory testing whether and how insights from optimal control theory and game theory can be applied to detailed spatiotemporal, stochastic, landscape-scale simulation models of the types used by regulators and plant health policy makers. The particular focus will be on how to control forest and/or crop diseases as effectively as possible, even when budgets and epidemiological knowledge are limited, while accounting for the hitherto underexplored effects of grower/manager behaviour in setting how epidemics play out in space and time.
Importance of Research
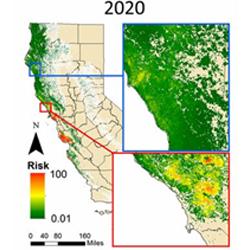
Increasing rates of global trade and travel, and changing climatic patterns, have led to more frequent outbreaks of plant disease epidemics worldwide. In forest ecosystems, non-native invasive pathogens routinely cause significant population, community, ecosystem and economic impacts. Contemporary examples include Phytophthora ramorum, the causal agent of sudden oak death in the United States and ramorum disease in the United Kingdom, as well as ash dieback (caused by Chalara fraxinea) across almost all of Europe. For crop diseases, taking just a single example, citrus production in the United States, Brazil and worldwide is threatened by several exotic pathogens, most notably citrus canker and citrus greening. Due to intensive research interest and particularly the availability of good epidemiological data, most notably detailed disease surveys at both local and regional scales, citrus is an excellent model system for food security threats to agricultural and horticultural crops more generally. For both types of system, what disease management has been attempted might perhaps be characterised as “too little too late”, driven largely by small budgets for disease detection & control. mathematical modelling can predict where and how invading pathogens will spread, as well as providing a rational methodology for comparing the performance of possible control strategies against one another. This project will consider how this approach – already used in practice by policy makers and regulators – can be made more realistic and more effective, particularly by properly accounting for individual behaviour.
Project Summary
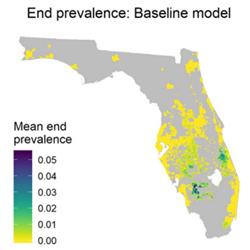
The conventional approach to optimise controls via a mathematical model – averaging an ensemble of simulations – is limited by computational power. The complexity of policy-relevant models (e.g. Cunniffe et al (2016)) and the vast array of controls/combinations of controls mean that only a small subset of all strategies can be fully tested. In contrast, the mathematics of optimal control theory can unambiguously select the strategy expected to offer the best mitigation of any given epidemic. However, the complexity of the mathematics means that it can only be applied to very simple models. A recent PhD project in my laboratory has shown how insights from optimal control theory might be practically useful, essentially by optimising via a simpler approximate model (Bussell et al (2019)). Continuing to develop this methodology to make these techniques directly useful for policy makers is the focus of part of this project. A second focus of the project focuses on extending results from a second, proof-of-concept, PhD project in my laboratory, which focuses on understanding how human behaviour affects plants disease epidemics (Murray-Watson et al (2022)). Growers and forest managers make decisions about which crops and/or trees to grow and when and where to plant them, as well as deciding whether and how aggressively to control disease. How this plays out at landscape scales is currently not well understood.
What will the successful application do?
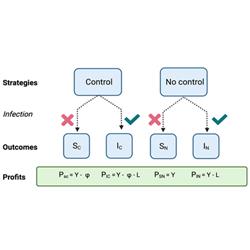
This project is based entirely on developing, fitting and using mathematical models. The student will build on recent large models of sudden oak death (Cunniffe et al. (2016)) and citrus greening (Mastin et al. (2020)), adding behavioural dynamics (Murray-Watson et al (2022)). The initial focus will be continuing to test model predictive control (Bussell et al (2019)) – in which optimal control is applied to a simpler approximation and then the optimal solutions are “lifted” back to the full simulation – in this more detailed setting. There are outstanding questions around the detail required in the approximate model, and which heterogeneities must be accounted for. A potentially very interesting area is how the complex and detailed control strategies that emerge from optimal control can be translated to the simpler strategies (essentially rules-of-thumb) appropriate for policy use. When epidemics are invading, it is also important to account for the unavoidable trade-off that emerges when attempting active control of an epidemic for which estimates of key epidemiological parameters become more precise only as the epidemic spreads and so becomes more difficult to control (Thompson et al (2018)). This important (and generic) tension will be a key focus of the work.
Training Provided
The student would learn:
i) mapping a complex biological system to a parsimonious mathematical model
ii) modern methods for simulating epidemiological models
iii) high performance computing, via use of the university’s HPC cluster
iv) experience of applying mathematics to a biological system
v) methods of fitting complex mathematical models to spatio-temporal data
vi) the mathematics of optimal control theory
The project would be well suited to a student with a background in mathematics, engineering, physics or theoretical ecology, ideally with prior knowledge of computer programming, motivated to transition to work on biological problems. However, students with a background in wet-lab biology have enjoyed and been very successful in my laboratory in the past. Any such candidates with a strong interest in making a transition to mathematical modelling are very much encouraged to get in touch to discuss.